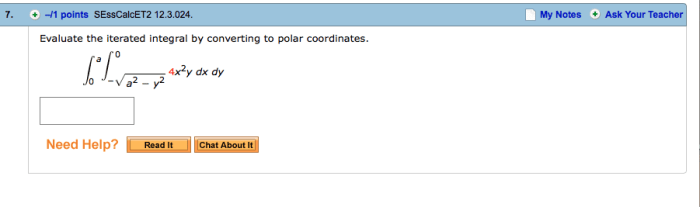
Evaluate the iterated integral by converting to polar coordinates – Evaluating iterated integrals using polar coordinates is a powerful technique that simplifies complex integrals and expands their applications. This comprehensive guide will delve into the intricacies of converting iterated integrals to polar coordinates, empowering readers to tackle challenging integrals with precision and efficiency.

Polar coordinates provide an alternative representation of points in a plane, introducing radial distance (r) and angular displacement (θ). By converting iterated integrals to polar coordinates, we exploit the inherent symmetry and simplify the integration process.

Evaluate the Iterated Integral by Converting to Polar Coordinates

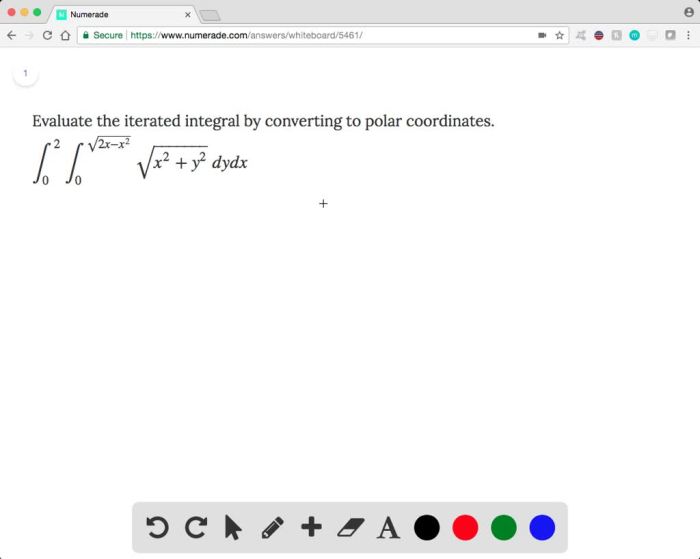
Iterated integrals involve integrating a function multiple times over different regions. Converting iterated integrals to polar coordinates can simplify the integration process, especially when dealing with regions defined by circular or radial boundaries.

Converting to Polar Coordinates, Evaluate the iterated integral by converting to polar coordinates

To convert an iterated integral to polar coordinates, we transform the limits of integration and the integrand in terms of polar coordinates. The following steps are involved:

1. Identify the region of integration and determine its polar coordinate representation.
2. Transform the limits of integration in terms of polar coordinates:
   • The lower and upper bounds of the radial integral become the minimum and maximum radii.
   • The lower and upper bounds of the angular integral become the starting and ending angles.
3. Replace the Cartesian coordinates (x, y) with polar coordinates (r, θ) in the integrand.

Evaluating the Integral

Once the integral is converted to polar coordinates, we can evaluate it using the following steps:

1. Integrate with respect to the radial variable (r) from the minimum to the maximum radius.
2. Integrate with respect to the angular variable (θ) from the starting to the ending angle.

Applications

Converting iterated integrals to polar coordinates finds applications in various areas, including:

• Calculating areas and volumes of regions bounded by circular or radial curves.
• Evaluating integrals involving functions that have circular symmetry.
• Solving problems in physics and engineering that involve cylindrical or spherical coordinates.

Tips and Tricks

Here are some tips and tricks for converting and evaluating iterated integrals in polar coordinates:

• Visualize the region of integration in polar coordinates to understand the limits of integration.
• Use trigonometric identities to simplify the integrand in terms of polar coordinates.
• Be careful when dealing with special cases, such as when the region of integration is not symmetric about the origin.

Essential Questionnaire: Evaluate The Iterated Integral By Converting To Polar Coordinates

What are the benefits of converting iterated integrals to polar coordinates?

Converting iterated integrals to polar coordinates simplifies the integration process, making it easier to evaluate complex integrals. Additionally, it allows for the exploitation of symmetry and the use of polar-specific integration techniques.

When should I use polar coordinates to evaluate iterated integrals?

Polar coordinates are particularly useful when the region of integration has a circular or symmetric shape. This is common in applications involving areas, volumes, and integrals over circular or annular regions.

How do I handle special cases when converting iterated integrals to polar coordinates?

Special cases arise when the region of integration includes points on the coordinate axes or when the limits of integration are not continuous. These cases require careful consideration and may involve splitting the integral into multiple parts.